Spinner

This one is a simple pattern that I added a zigzag of triangles.
I'll have to get back to this in a bit--it needs a few pictures to exaplain...

Shells

Maybe tomorrow I'll spiral this one but today I'll stick with concentric rings. The shells made of pentagons are decorated with triangles. The program that made this is not too sophisticated I think that when I try to make a spiral design I'll have to do a little more tinkering.... You'll just have to wait and see.

Heptagon Mix

I was thinking about doing this pattern with heptagons. The problem is that in the old pattern three pentagons fit around a vertex with room to spare but three heptagons do not fit around a vertex. To make room, I inserted two squares and was off to the races. Also, I threw in some triangles to add some variation into the mix. Perhaps this would look a bit more interesting if I added some alternation of colours.... To make an better backdrop, after I cut out the rectangular part that will generate the pattern, I load it into gimp (a linux knockoff of photoshop) and fade the colours (using about a 0.4 alpha on a white background).

Jungle

I'm not sure why I'm calling this a jungle. This pattern is a variant of the one on Tuesday, August 15, 2006. The pattern comes from putting a zig-zag of triangles into every loop in the original. For instance, the original has loops or six pentagons that form a rhombus hole in the middle. Here the rhombus is transformed into curved triangles (the triangle in the middle is just for decoration). On close examination, There are still only two orientations of the pentagons--half the pentagons have a vertical side.

Birds

Perhaps I'm being a bit optimistic that people can see birds. The gaps that are not rhombic (like a diamond) remind me of birds. In the pattern, I see these birds circling around in big spirals. The program that generates this is a very short recursive program. The pentagons alternate between gray and orange. I was a bit surprised at first that there was only alternating colours in the pattern. Even though I programmed the colours to alternate, I am really only programming the polygons to fan in a tree-like fashion. There could be many incidental connections that occur. But on further inspection, all the loops have an even number of polygons so it would be impossible to have two of the same colour. In fact, since each colour represents a particular orientation two pentagon of the same colour can't share just one edge (they would have to share all five or none).

Clover?

I'm calling this pattern clover because of the negative space. Looking at the polygons though, it reminds of some sort of the three legged wheel that I saw in a weird movie... This pattern was developed using a zigzag technique similar to yesterday. The three squares zig one way then the other as they go from hexagon to hexagon.

Zigzag Grid

This one is not too inspired but...deal with it. It follows a similar construction to this one except the zigzagging here is with heptagons and the grid uses hexagons in the same layout as the the triangular grid (each hexagon only has edge connections with three hexagons rather than six). This is also similar to this construction. Perhaps the decorative red triangles should be a different colour....

bunny

I'm bringing it down a notch. Here's a simple bunny. The only tricky thing with this pattern is that there are unseen polygons (a hexagon and two squares) used to place the eyes, nose, and mouth. See if you can make a better bunny.

Embellishing Octagons

This pattern started out as a loop of octagons that was turned inside out with two loops of two hexagons, four squares (green), and two triangles. This inside-out loop served as my main loop which is the one that doesn't have the pentagons in the middle of it. After, I fit these loops together let a checker board. I filled other loops that were constructed with some yellow squares, triangles, and some pentagons.

The images below can be used as wallpaper. There are links to images that are 323x323 pixels. Perhaps they would look better smaller...

Just a simple pattern for a Monday morning. This pattern began as a triangular grid and then two pentagons were inserted between each pair of triangles. Finally, the newly created loops were decorated with some more triangles making the boxy looking stars in the middles of the loops.

Here's a polygon pattern that relies on a simple recursive call. Each heptagon attaches to two scaled down heptagons and each of those heptagons attaches to two more etc. This recursive definition is easy to do in PolygonR&D. The tightness of the spiral is determined by the main shrinking factor--the difference in size of the heptagon to the next biggest heptagon.

Once again I am playing with negative space--the pattern seems more about the four-point stars than the pentagons. This pattern (with different the colouring) is on the cover of the Tilings and Patterns: An Introduction (A Series of books in the mathematical sciences) by Branko Grunbaum and G. C. Shephard which is a great book. The last couple of blog entries have convinced me to slightly augment the language of the programming language of PolygonR&D to make the programs slightly easier to write. I'll let you know if it was worth it....

Here's another spiral. This is made with nonagons (nine-sided polygons) and has three arms. Some difference between this one and the one yesterday is that the banana-shaped gaps are bigger and they have eighteen orientations instead of fourteen. Close to the centre of the pattern like the image to the left it appears curved like a true spiral but a bigger image would reveal the eighteen-sidedness. To show that there is no trickery about the nonagons nicely fitting together there is a close up included below.

Here's a spiral pattern made of heptagons. The fours groups of banana gaps between the heptagons form the four arms of the spiral. With close examination of the gaps, one can find fourteen different orientations, which are grouped together in wedges similar to the last pattern with alternating pentagons. This pattern was created using a short PolygonR&D program (50 lines for this two colour pattern or 15 lines if it were all blue).

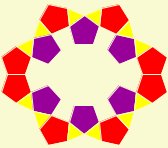
This pattern alternates two different orientations of pentagons. The pointing up ones are blue and the pointing down ones are purple. Notice that all but one of the pentagons (the central pentagon) are connected to exactly three other pentagons. The pattern can be thought of as concentric rings of pentagons (that will approximate decagons). Another way to understand the pattern is by grouping rhombi (the white diamond slivers) in terms of orientation--there are five different orientations. The rhombi form ten wedges that meet at the central pentagon.

This pattern is somewhat like Friday's pattern in that it uses some sections of a big loop inverted to make a loop with a star shape. The pattern alternates heptagons and triangles with the exception of the orange hexagons in the middle (heptagons didn't fit). It also has a flavour of August first's pattern since it has the same type of rotational symmetry. I prefer the August first because it offers a lot of the same interesting lines yet with a simpler design.

After a big battle with aesthetics, I finally settled on this pattern that makes a nice wall paper background (the image on the right). I'll highlight some of the battle. I originally started with a two colour pattern with just pink and purple. I thought it would have more impact than it did but I think with the regularity of the colouring that the pattern was dull. I added some colour it to make its bigger loops of twelve octagons and twelve triangles stand out. Even after I added orange to the mix it seemed too regular. The I introduced a twist to the pink loops of six octagons. To show you these transitions I'll added the pictures below. The key to recognizing the differences is to examine the negative space especially the asterisk like shapes. Notice there are two orientations in the pattern above as opposed to below where there is only one.

I guess that I've been a bit obsessed with pentagons and triangles recently. This is mostly an alternating pattern but has a couple of hexagons and triangles. I guess I like this one because of the central curved pentagon. I wish I was able to find a better way to fill the inside of the outer loop...

Here's a little play with hexagons and pentagons. Basically, the outside loop comes from this big loop below. The rest is mere decoration. The pentagon in the middle was difficult to place(and may not be at the theoretical centre).

This quickie pattern uses a simple section that combined with a bunch of mirrors creates a nice grid. Unlike the latest previous pentagon and triangle patterns, this does not have an alternating of the polygons. Below is a section that will produce this pattern as wallpaper.

Sunflower

This pattern of a sunflower was a bit tricky to construct. The outer orange section (the petals) was easy given the high level of repetition but filling the insides (the seeds) was not straight forward. The pattern is built with alternating pentagons and triangles. The five-fold symmetry is present throughout the pattern.

This pattern is like the August first pattern: orange nonagons are used instead of heptagons. There are four more nonagons eight more triangles. The pattern arises from wiggly loop of nonagons that have been interlaced with a straight line of triangles. The inner and outer triangles that decorate the pattern help bring out its nine-fold symmetry.

This pattern came about by elaborating a loop of interleaved triangles and squares. Each of the six loops on the outside of the central hub comes of a loop of squares and triangles where three of the triangles have been replaced with hexagons. The hexagons introduces spaces in the loops so that they can easily be connected (with squares) to one another while maintaining the original angles of the replaced triangles. As well, there are additional hexagons put in the central hub to make the negative space more eye catching.

This pattern applies the concept of a five point star to heptagons. The five point star
can be constructed with a pentagon path that alternates a small turns to the right followed by a larger turns to the left. For heptagons, there are fourteen polygons instead ten. As well, the purple triangles and pentagons are added to the loop fourteen heptagons for decoration. I think that these extra polygons help bring out the symmetry.

Here's another unravelled loop. A graphical representation of the process of creation is below. A pentagon loop (two partial stars) is combined with two loops of six triangles. The two gaps between the adjacent red pentagons are not filled with triangles (notice that there was originally fourteen gaps in the original loop and only twelve triangles)--these gaps are filled with squares and that are decorated with purple pentagons to maintain the alternating colours.

* = ...

This one began as a simple loop of six pentagons that was turned inside-out using two loops of three pentagons. Afterwards to link those inside-out loops (which look perhaps like a toothy mouth) another loop was used--the original simple loop of six pentagons was elaborated with interlacing hexagon spacers (these loops inner hole look like the outlines of eights with a vertical javelin through it). Below, I included a wallpaper version of the pattern.

Sometimes it's the missing tiles that make things interesting. Here there are a number of missing heptagons. A missing heptagon makes each of the gentler curve between the three triangles. Including the heptagons would lead to many overlapping polygons. Perhaps there is an artful inclusion of a selection of the heptagons...

This is constructed by interleaving a loop of fourteen orange heptagons with a straight line of olive triangles. As well fourteen additional triangles decorate the inside and outside of the new loop.