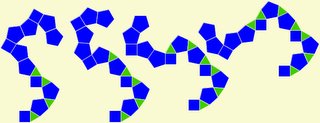
Large symmetrical loops made with pentagons make this pattern interesting. In the inner loop, there are ten pentagons with ten square spacers that outline a twenty-sided regular (all angles and sides are the same) polygon. In the outer loop, there is a thirty-sided regular polygon which can be seen as the diagonals of the grey triangular pairs.